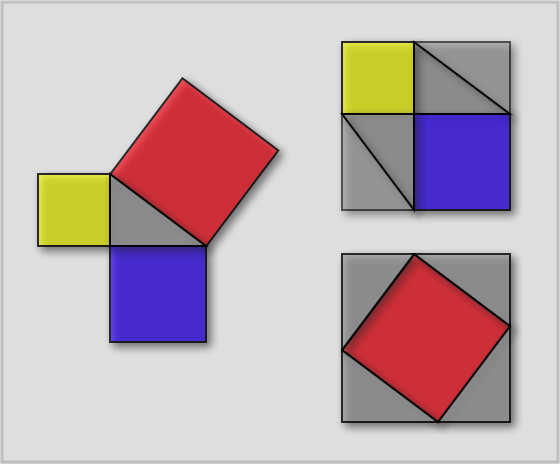
Euclid of Alexandria proved that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the two sides. Here are two pictorial demonstrations. The first is a version of a Chinese proof by dissection that dates from 200 BC to 200 AD. In the diagram below at left, we wish to show that the area of the red square is equal to the sum of the areas of the yellow and blue squares.

We construct the figure at the upper right by removing the red square from the figure at left and filling in the large square that circumscribes the yellow and blue squares. This is accomplished by adding three gray triangles, each of them congruent to the gray triangle in the figure at left. The figure at the bottom right is obtained by removing the yellow and blue triangles from the figure at left, and adding three more gray triangles.
The second demonstration is by tessellation:

Left: We've tiled the plane in two ways. First with blue and yellow squares whose sides represent the sides of a right triangle. Second with diagonal squares, one of them pictured in red, whose sides are equal to the hypotenuse of the original triangle.
We see that any given portion of a plane tiled in this way contains the same number of red, yellow, and blue squares, and the result is established.

Right: We can rearrange the pieces of the complete yellow and blue squares to form a complete red square.

First, move the triangular part of the yellow square that is outside the red square to the lower left part of the red square, as shown.

Next, move the large trianglar portion of the blue square that is outside the red square to the upper left part of the red square, as shown.

Finally, move the remaining small blue triangle that is outside the red square to the upper right part of the red square, as shown. The rearranged portions of the yellow and blue squares completely fill the red square, and the result is established.
Source: The Pythagorean Theorem: A 4,000 Year History, by Eli Maor