a problem involving π

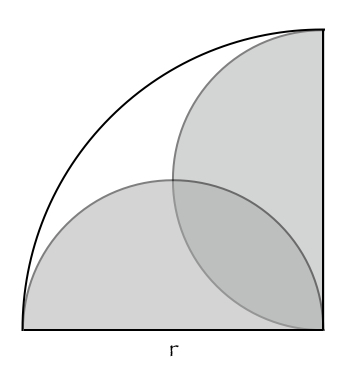
To show: The white area inside the figure is equal to the dark gray area.

We first observe that the entire figure is one quarter of a circle of radius r and that the two semicircles taken together form a circle of radius r/2.

We're now ready to write a couple of equations:

 area of entire figure = (white area) + (light gray areas) + (dark gray area) = (1/4)πr²

 area circle of radius r/2 = (light gray areas) + 2(dark gray area) = π(r/2)² = (1/4)πr²

Subtracting the second equation from the first, we have

 (white area) − (dark gray area) = 0

or

 (white area) = (dark gray area)

QED

Source: The Tokyo Puzzles by Kobon Fujimura